[DL] 선형회귀, 활성화 함수, 로지스틱 회귀
세상에는 많은 종류의 데이터가 있다.
우리는 데이터를 모아서 알수 없는 함수 f* 를 근사하고 싶어 한다.
> 그렇다면 어떤 모델로 그 함수를 근사할 수 있을까?<
선형계층이 이 질문에 대한 해답이다..
선형 계층은 심층신경망의 가장 기본 구성요소가 되며
뿐만 아니라 하나의 함수로 볼 수 있다.
예를 들어 아래 사진과 같이 4개의 입력을 받아 3개의 출력을 반환하는 함수로 생각할 수 있다.
y =f ( x ) =x ⋅W + b
이 모델 함수는 위 식과 같이 가중치 파라미터에 의해 동작이 정의된다.
즉, 모델은 와 를 가중치 파라미터로 갖고 있다는 말이다.

모델의 가중치 파라미터들의 집합을 이제 고 표현하도록 하겠다.
θ ={ W ,b }
이름이 선형계층이듯이 선형관계 데이터를 주로 나타낼 때 사용이 된다.
예를 들어 키와 몸무게를 생각해보자.
보통은 키가 크면 몸무게가 많이 나간다.
또는 공부량과 성적간의 관계를 생각해보면 마찬가지다.
이러한 관계를 "선형 관계"라고 말한다.
선형회귀
선형적 관계를 가진 데이터들을 예측하는 문제를
선형회귀라고 부른다.
아래 사진을 보자

파란색 점이 실제 데이터를 의미하며
빨간 점선은 이러한 파란색 점들의 선형 관계를
나타내는 f이라고 할 수 있다.
우리는 f를 근사계산하는 것이 목표이며(즉 f과 비슷한 함수를 구현)
그러기 위해서는 f의 함수값과 차이(손실값)가
최소가 되는 가중치 파라미터를 찾아야 한다.

데이터셋 는 N개의 n차원 입력 벡터들과 N개의 m차원 타겟 출력 벡터들로 구성되어 있다.
n차원의 데이터를 가져와 선형 회귀 모델(선형계층)에 통과시키면,
m차원의 출력 데이터 y_을 얻을 수 있다.
이렇게 모델로부터 얻어진 y_를
실제 타겟 벡터와 비교하면 손실 값(loss)을 얻을 수 있게 된다.
( Loss = f*(실제값) - f(예측값) )
이 손실값(Loss)는 선형회귀모델에 따라 달라지기 때문에,
즉 선형회귀 모델의 파라미터가 무엇이냐에 따라 달라지기 때문에
손실값은 가중치 파라미터에 따른 함수로 볼 수 있다 (=> 손실함수)
따라서 이 손실값을 최소화시키는 가중치 파라미터를 찾기위해서
이 손실 값을 가중치 파라미터로 미분하게 되면
손실 값을 낮추는 방향으로 파라미터를 업데이트 할 수 있게 된다.
이와 같은 작업을 가중치 파라미터가 수렴할(더이상 바뀌지 않을) 때까지 반복하면,
손실 함수를 최소화시키는 가중치 파라미터를 구할 수 있게 된다.
결과적으로 손실 함수를 최소화하는 가중치 파라미터를 가진 선형 회귀 모델 는
우리가 근사하고자 하는 함수f*와 유사하게 동작할 것이다.
계속 위에서 손실함수를 말했는데,
손실함수는 실제값과 예측값의 차이를 정의하는 함수로
손실값이 작을수록,
우리는 원하는 출력 값과 모델이 반환한 출력 값의 차이가 작다는 것이고
이는 우리가 구현한 함수가 좋은 모델이라고 판단할 수 있는 지표가 된다.
즉 N개의 데이터가 있고
우리가 이 N개의 데이터를 잘 예측하는 함수 fθ를 구현했다고 했을 때
손실함수는 아래와 같이 정의할 수 있다.
(어떤 손실함수를 사용하냐에 따라 조금씩 달라지겠지만..!
아래는 L1norm을 사용한 손실함수이다 )
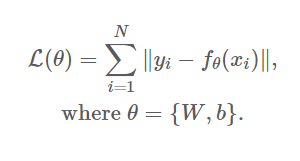
위 식을 보면 손실함수는 결국 fθ에 의해 달라지는 것을 확인할 수 있다.
왜냐면 yi와 xi는 이미 정해진 값이므로
결국은 fθ, 즉 W와 b의 값이 무엇이냐에 따라 달라지기 때문에
W와 b를 어떤 값으로 설정하냐가 중요한 관건이라는 것이다.
손실함수에는 여러가지 함수가 있지만,
선형회귀의 손실함수로는 주로 MSE 또는 RMSE를 사용한다.
MSE
Mean Squared Error로, 평균 제곱 오차를 의미한다.
주로 선형회귀의 손실함수로 사용한다.
즉 (실제 함수값 - 예측값 ) 제곱의 평균을 의미하는 것이다.

RMSE
rmse는 mse에 루트를 씌어준 것이다.

선형회귀 말고 대표적인 회귀로는 로지스틱회귀 또한 있다.
로지스틱 회귀를 이야기 하기 전에 활성화 함수에 대해 정리해보고자 한다.
활성화 함수
대표적인 활성 함수로는 시그모이드와 하이퍼볼릭 탄젠트(탄에이치)가 있다
아래는 이 두함수를 그래프로 나타낸 것이다.

시그모이드 함수의 출력 값의 범위는 0에서 1사이이며,
탄에이치의 경우에는 -1에서 1사이이다.
두 함수 모두 전 구간에서 미분 가능하며,
그림에서 알 수 있듯이 양 극단의 기울기는 0에 근접하는 것이 특징이다.
두 함수를 수식으로 나타내면 다음과 같습니다.

경우에 따라, 는 활성 함수 자체를 의미하기도 한다.
로지스틱 회귀
선형 회귀의 경우에는 키와 몸무게와 같은 선형 데이터의 관계를 다루었다.
즉, n차원의 실수 벡터를 입력으로 받아
선형 관계의 m차원의 실수 벡터를 반환하도록 학습하는 문제였다.
> 그렇다면 로지스틱 회귀의 경우에는 어떤 문제에 적용할 수 있을까? <
실제 어떤 수치를 예측하는 것도 좋지만
우리는 어떠한 결과값이
참인지 혹은 거짓인지를 예측해야 하는 경우도 생각해봐야 한다.
예를 들어 어떤 사람의 신상 정보( 키, 몸무게 등)가 주어졌을 때,
"키가 000cm일 때 몸무게가 몇 kg인가?"에 대한 해답이 아니라
“그 사람이 남자인가?”라는 물음에 대한 대답을 구하는 문제를 생각해볼 수 있다.
이럴 경우 만약 그 사람이 남자인 경우에는
함수 f* 는 참을 반환하고,
여자인 경우에는 거짓을 반환할 것이다.
이 경우에는 기존 선형 회귀로 문제를 풀기보단
다른 방법으로 접근해보는 것이 나을 것이다.
이때 필요한 방법이 로지스틱 회귀 방법이다.

사실 선형 회귀 문제를 풀기위한 선형 계층 함수의 구성과 크게 다르지 않다.
다만, 선형 계층 함수 직후에 활성화 함수인 시그모이드함수를 넣어주어 전체 모델을 구성해야 한다.
그럼 이 모델의 출력 값의 범위는 무조건 0에서 1사이로 고정될 것이다.
이 점을 활용하여 우리는 참/거짓을 예측할 수 있다.
( 예를 들어 0.5초과이면 참, 미만이면 거짓 )
로지스틱 회귀는 선형회귀와 비슷하기 때문에 학습하는 법 또한 매우 비슷하다.

데이터 샘플들을 모델에 통과시키면, 예측 결과값을 얻을 수 있다.
이 예측 결과값과 실제 함수값과 비교하면 손실 값을 계산할 수 있다.
여기서 선형 회귀와 마찬가지로 손실 값을 가중치 파라미터로 미분하게 되면,
손실 값이 낮아지는 방향으로 경사하강법을 수행할 수 있게 된다.
경사하강법을 통해 모델 가중치 파라미터를 업데이트 하는 작업을 반복하게 되면,
점진적으로 손실 값은 낮아질 것이고 점차 수렴하게 될 것이다.
그럼 우리는 수렴한 가중치 파라미터를 통해 f* 를 근사한다고 볼 수 있다.
참고로 이때 손실 값을 계산하기 위한 손실 함수는 선형 회귀와 달리 MSE 손실 함수를 사용하지 않는다.
로지스틱 회귀는 이름은 회귀이지만 사실 회귀 문제가 아니라 분류 문제이다.
왜냐면 최종 결과값으로 어떠한 수치를 반환해주지만
이는 결국 참과 거짓으로 변환이 되기 때문이다.
따라서서 우리는 로지스틱 회귀를 확률과 관련된 문제로 연관지어 생각할 수 있고,
이것은 기존 회귀와 다른 손실 함수를 써야 하는 이유이다.
그래서 우리는 로지스틱 회귀와 같은 이진 분류문제를 풀기 위해서는
이진 크로스엔트로피, BCE 손실 함수를 사용한다.
코드 구현
아래 코드는 로지스틱 회귀를 코드로 구현한 것이다.
#로지스틱 회귀 이므로 시그모이드 함수 이용해야함 (즉, nn.linear()를 그대로 적용하면 안된다)
# 사용자 정의의 로지스틱 회귀 모델 생성
class MyModel(nn.Module): #nn.Module을 상속 받고자 함 -> init이랑 forward
def __init__(self,input_dim,output_dim): #필요한 기능 구현
self.input_dim=input_dim
self.output_dim=output_dim
super().__init__() #nn.module의 기능 사용 가능
self.linear=nn.Linear(input_dim,output_dim) #선형계층
self.act=nn.Sigmoid() #활성화함수로 시그모이드사용 -> 선형 회귀와 다른점
def forward(self,x): #기능 실행 함수
y=self.act(self.linear(x)) #선형계층 함수 적용 후 시그모이드 적용
return y
선형 회귀는 nn.Linear를 통해 구현할 수 있다.
input으로 input 크기와 output크기를 넘겨주면 된다.
( 예를 들어 3차원을 2차원 데이터로 변환하고 싶으면 : nn.Linear(3,2) )
model=nn.Linear(x.size(-1),y.size(-1))