[DL] 심층신경망 Basic
이미지, 음성, 텍스트등과 같은 데이터들은
비선형 데이터일 뿐만 아니라 높은 차원의 데이터이다.
선형 모델로 이러한 데이터들을 다루는 데에는 한계가 존재
이러한 문제들을 심층신경망이 해결할 수 있다.
심층신경망?
비선형 데이터를 풀기 위해서 계층을 깊게 쌓아올린 것이다.
이때 서로 다른 선형 계층을 깊게 쌓아 구성할 수 있다.
이때, 여러개의 선형 계층을 쌓아올려봤자
결과로 또 다른 선형계층이 나올 뿐..!
따라서 이러한 방법으로는 비선형 문제를 풀 수 없다.
>그렇다면 어떻게 해결할 수 있을까?<
간단한 방법으로는 선형 계층을 쌓을 때
그 사이에 "시그모이드"나 "탄에이치"와 같은 활성화 함수,
즉 비선형 함수를 끼워 넣으면 된다.

심층신경망의 너비와 깊이를 조절하여
더욱 더 복잡한 데이터를 다룰 수 있다.
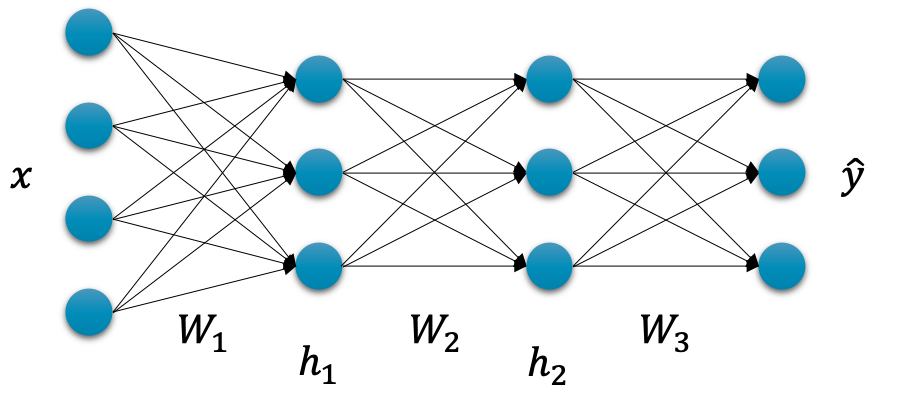
보통 신경망을 구성할 때는
아래 사진과 같이 너비가 줄어드는 형태로 구성한다.
(아래 사진에서는 4차원 데이터를 3차원 데이터로 변환)
또한 깊이를 깊게, 즉 계층을 더 많이 쌓아 올릴 수록
더 복잡하고 어려운 데이터를 풀 수 있다.

이와 같이 신경망의 너비와 깊이를 조절하여
다양한 데이터를 효율적으로 다룰 수 있기에
적절한 너비와 깊이를 선택하는 것이 매우 중요하다!
>심층신경망 학습은 어떻게 할까?<
딥러닝의 근본적인 목표는
실제 함수 f에 근사하는 f*를 구성하는 것이다.
즉, f*를 통해 나온 결과값과 실제함수값의 차이(손실값) 가
최소가 되어야 한다.
즉, 우리는 손실값이 최소가 되는
손실함수의 입력 가중치 파라미터를 찾아야 한다.
여기서 사용하는 방식이 경사하강법이다.
경사하강법은 손실함수를 가중치 파라미터로 미분하여
손실값이 낮아지는 방향으로 가중치 파라미터를 업데이트 하는 방식이다.
아래 사진을 보자!

D는 데이터를 의미한다 (x,y)
x데이터가 심층신경망을 거쳐서 나온 데이터를 y_라 하자(흰색 상자 데이터)
y_과 y데이터간의 차이를 Loss, 즉 손실값이라 부르며
손실값은 가중치 파라미터에 따라 달라진다.
( f*이 선형회귀라면 f*=W x + b로 나타낼 수 있는데, 여기서 가중치 파라미터는 W와 b를 의미
y_은 여러개의 함수(심층신경망이기 때문에)를 거쳐서 나온 값이기 때문에
결국 손실값 또한 W와 b에 영향을 받음 )
우리는 손실함수가 최소값이 되도록 하는 것이 목표이므로
경사하강법을 이용하여 손실함수를 가중치 파라미터로 미분한뒤,
손실값이 낮아지는 방향으로 (함수의 극소값쪽 방향으로) 업데이트 해야한다.
근데 우리는 심층신경망이다. 즉 이말은, 계층이 여러개인 만큼
가중치 파라미터도 늘어나게 된다는 뜻이다.
즉 그러면 미분 해야하는 일도 늘어난다는 것을 의미한다.
역전파
우리는 역전파 알고리즘을 통해
효율적으로 심층신경망을 학습시킬 수 있다
역전파 알고리즘은 체인룰(Chain Rule)을 통해 구현이 된다.
xi를 입력으로 받아 첫번째 계층을 지나면 h1,i가 나올 것이고
이후 계속해서 이어지는 선형 계층과 활성화 함수를 통과하게 될 것이다.
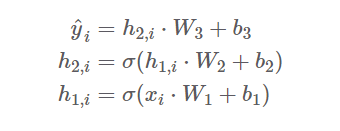
우리가 해야 할 일은 각 가중치 파라미터 별로 손실함수를 미분하고
결과를 바탕으로 각 가중치 파라미터를 업데이트해야 한다.

문제는 업데이트를 하기 위하여
손실함수를 각 가중치 파라미터로 미분을 하는 것인데,
이 과정은 매우 비효율적인 일이다.
이에 우리는 역전파 알고리즘( 즉, 체인룰을 이용 )을 활용하여 손쉽게 구현할 수 있다.
아래 사진을 보자!

첫째 줄은 손실함수를 W3으로 미분한 과정을 보여준다
두번째 줄은 W2로 미분한 과정을 보여주고,
세번째 줄은 손실함수를 W1로 미분한 과정이다.
각 과정마다 겹치는 부분도 있고
h를 W로 미분하는 과정은 간단하게 계산할 수 있기에
역전파 알고리즘을 이용하여 훨씬 효율적으로
심층신경망을 학습시킬 수 있다.

>심층신경망이 너무 깊어지면?<
심층신경망이 너무 깊어지면
입력에 가까운 계층의 가중치 파라미터가 잘 업데이트가 되지 않는
그래디언트 소실이 발생할 수 있다.
그래디언트 소실
아까 위에서 심층신경망을 구성할 때
선형 계층 사이에 활성화 함수를 넣는다고 했다

위 사진은 활성화 함수, 시그모이드 함수(파란색)와 탄에이치(빨간색)을 나타낸 것이다.
이 함수들을 미분하면 시그모이드는 1보다 작은 값을,
탄에이치는 1보다 작거나 같은 값을 가진다.
만약 계층이 40층이고, 활성화 함수를 여러번 통과한다면
손실값을 미분할 때
1보다 작은 값들을 계속 곱해야 하는 상황이 발생하게 된다.
그렇게 되면 거의 0에 근접하게 되어
입력에 가까운 계층의 가중치 파라미터는 업데이트 양이 거의 없게 될 것이다.
이처럼 입력에 가까운 계층이 잘 학습되지 않는 문제를
그래디언트 소실이라고 부른다.
렐루(ReLU)
그래디언트 소실은 활성화 함수의 미분 값이 1보다 작아서
발생하는 문제라고 볼 수 있다.
Relu는 이러한 기존 활성 함구의 단점을 보완하기 위해
제안된 새로운 활성화 함수이다.

음수 구간에서는 전부 0의 값을 가지고,
양수 구간에서는 전부 기울기가 1인 형태가 된다.
하지만, 음수 구간에서 전부 0이기 때문에 만약 렐루의 입력값이
전부 음수라면 가중치 파라미터들이 학습 과정에서
영원히 업데이트될 수 없는 문제가 발생하게 된다.
이러한 문제를 해결하기 위해 나온 것이 리키 렐루이다.
리키렐루 (Leaky ReLU)

ReLU의 단점을 보완하여
음수 구간에서 비록 1보다 작지만
0이 아닌 기울기를 갖는 것이 특징이다.
렐루의 단점을 보완했다고 해서
리키렐루가 무조건 좋은 것은 아니다.
상황에 따라 더 적합한 활성화 함수를 선택해야 한다.
또한 렐루와 리키렐루를 사용하더라도
음수 구간은 여전히 기울기가 1보다 작기 때문에
그래디언트 소실 문제가 완전히 해결된 것은 아니다!
코드 구현
#심층신경만 구현
class Mymodel(nn.Module): #nn.module을 상속받음
def __init__( self,input_dim,output_dim): #필요한 변수나 기능 선언(활성화함수, 선형계층함수, 입력 차원 등등)
self.input_dim=input_dim
self.output_dim=output_dim
super().__init__() #torch.nn모듈을 사용할 수 있게끔 해줌- > nn.module호출
self.linear1=nn.Linear(input_dim,3) #선형계층
self.linear2=nn.Linear(3,3)
self.linear3=nn.Linear(3,3)
self.linear4=nn.Linear(3,output_dim)
self.act=nn.ReLU() #활성화 함수
def forward(self,x): #함수실행
h=self.act(self.linear1(x))
h=self.act(self.linear2(h))
h=self.act(self.linear3(h))
y=self.linear4(h)
return ynn.module을 상속받는 class를 통해 심층신경망구현할 수도 있지만
nn.sequential 함수를 이용하여 심층신경망을 구현할 수도 있다.
#위와 같이 함수로 구현할수도 있지만 nn.sequential을 통해도 구현 가능
model=nn.Sequential(nn.Linear(x.size(-1),3),nn.LeakyReLU(), #선형함수와 활성화 함수 따로 선언
nn.Linear(3,3), nn.LeakyReLU(),
nn.Linear(3,3), nn.LeakyReLU(),
nn.Linear(3,3), nn.LeakyReLU(),
nn.Linear(3,y.size(-1)))
앞에서 배운 경사하강법을 적용하여 최적화 시켜보자
#최적화
learning_rate=1e-4
n_epochs=200000
print_intervals=10000
optimizer=optim.SGD(model.parameters(), lr=learning_rate)
for i in range(n_epochs):
y_hat=model(x)#예측값 반환 (첫번째 epocj이후에는 update된 W,b를 이용하여 예측)
loss=F.mse_loss(y_hat,y) #손실값 계산
optimizer.zero_grad()#update된 파라미터의 미분값 초기화
loss.backward() #가중치 파라미터들에 대한 편미분(W,b)
optimizer.step() #가중치 파라미터 update (이 값은 다음 epoch때 사용)
if (i+1)%print_intervals == 0 :
print('Epoch %d: loss=%.4e' %(i+1, loss))
결과를 보면 손실값이 점점 줄어든 것을 확인할 수 있다.
이번에는 실제값 y와 예측값 y_hat의 관계를 그래프로 확인해보자!
df=pd.DataFrame(torch.cat([y,y_hat],dim=1).detach().numpy(), columns=['y','y_hat'])
sns.pairplot(df)
보면 선형관계임을 확인할 수 있다.
즉, 거의 근사하게 예측을 했다는 것이다!