이제까지 우린 학습 데이터로부터 손실 값을 구해서
모델의 학습 여부를 판단했다.
이를 다른 표현으로 학습 오차라고 부른다.
>그런데 만약 학습 데이터에 잘못된 레이블이 있다면..
또는 의도치 않게 편향이 존재한다면 어떻게 될까?<
즉, 잘못된 레이블까지 신경망이 학습했다면 어떻게 될까?
그럼 실제 배포된 상황에서도 모델이 잘못된 정답을 뱉어낼 수도 있을 것이다.
좋은 인공지능이란 일반화를 잘하는 인공지능이다.
일반화란 보지 못한 데이터에 대해서 좋은 예측을 하는 것을 의미한다.
세상 모든 데이터를 모델에 입력을 하면
모델은 입력값에 대응하는 결과값을 찾아서 반환만 해주면 되기때문에
오차가 발생할 수 없다.
하지만 모든 데이터를 학습시킬 수 없으니
우린 일부 데이터만을 가지고 모델을 학습하여
학습된 모델을 통해 학습시키지 않은 데이터 (보지 못한 데이터)에 대해서 예측을 해야 한다.
따라서 우리는 학습 오차를 최소화 하는 것이 최종 목표가 아니다.
우리의 최종 목표는 일반화 오차를 최소화 하는 것이 최종 목표이다.
오버피팅
오버피팅이란
‘학습 오차가 일반화 오차에 비해서 현격하게 낮아지는 현상’을 말한다.
즉, 학습 데이터에 편향이나 노이즈가 있을 때,
이것까지 모델이 학습함으로써
오히려 모델이 일반화를 수행하는데 방해되는 상태를 의미한다.
>그렇다면 언더피팅은 무엇일까?<
언더피팅은 오버피팅의 반대를 의미한다.
언더피팅이란 '모델이 충분히 데이터를 학습하지 못하여,
학습 오차가 충분히 낮지 않은 현상'을 이야기한다.
보통 모델의 수용능력이 부족하여,
복잡한 데이터의 관계를 학습하지 못하는 경우에 많이 발생한다.
우리는 오버피팅과 언더피팅 여부를 통해 우리의 최종 목표에 잘 도달하고 있는지 확인할 수 있다.
특히 오버피팅의 경우에 우리가 무조건 오버피팅을 피해야 하는 것이라기보단,
오버피팅은 모델의 수용능력을 나타내는 좋은 지표로 활용되기도 한다.
예를 들어, 오버피팅이 발생하였다는 것은
모델의 수용능력이 데이터의 복잡한 관계를 학습하기에 충분하다는 이야기가 될 수 있고
오버피팅 여부를 확인한 이후에
오버피팅을 방지하는 방향으로 모델을 개선하면 되기 때문이다.
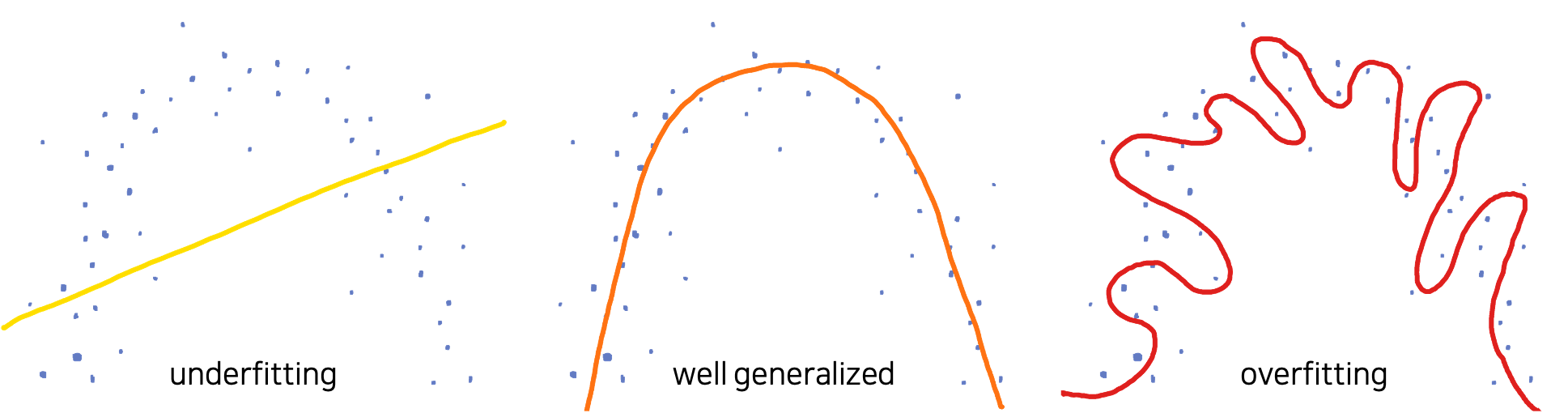
예를 들어 위와 같이 분포된 데이터를 수집했을 때,
우리의 목표는 이 데이터를 생성해낸 어떤 알수 없는 함수 를 근사하는 것이다.
하지만 그림에서 확인할 수 있듯이 이 데이터셋은 편향 또는 노이즈를 포함하고 있기도 하다.
이때, 왼쪽과 같이 선형 모델로 이 데이터를 모델링하고자 한다면 잘 동작하지 않을 것이다.
선형 모델은 이 데이터를 학습하기에 너무 수용능력이 작기때문이다.
따라서 이러한 경우에 언더피팅이 발생하게 된다.
또는 오른쪽 그림과 같이 너무 복잡한 형태의 함수로 근사할 수도 있을 것이다.
하지만 이 경우에는 아마 지나친 일반화가 이루어진것이라고 볼 수 있고,
(너무 파란점에 지나치게 학습이 되어있음)
이에 학습 오차는 낮을 수 있지만 일반화 오차는 높은 상태인 오버피팅이 발생했다고 판단할 수 있다.
그러므로 우리는 가운데와 같이 어느정도 노이즈가 편향이 있음을 감안하였을 때,
데이터를 간단하게 일반화 할 수 있는 2차 함수 곡선의 형태로 함수를 근사할 수 있을 것이다.
검증(Validation)
만약 모델의 최적화가 잘 수행되고 있고 모델의 수용능력이 충분하다면,
학습 초반에는 보통 언더피팅으로 시작해서 어느순간 오버피팅으로 전환될 것이라고 생각해볼 수 있다.
즉 초반에는 중요한 데이터의 특징들을 배우다가,
어느순간부터 학습 데이터의 불필요한 특징들까지 학습되는 순간이 올텐데,
이것을 잘 감지하고 오버피팅으로 전환되는 순간에 학습을 멈춘다면
아마 가장 이상적이라고 볼 수 있을 것이다.
이러한 역할을 검증 데이터셋을 도입함으로써 수행할 수 있다.
앞서 언급한 것처럼, 우리는 일반화 오차를 최소화 하는 것이 최종 목표이다.
따라서 만약 모델이 오버피팅이 발생하지 않았고,
검증 데이터셋이 학습 데이터셋과 같은 성질(분포)을 갖고 있다면,
모델은 검증 데이터셋에 대해서도 비슷한 손실값을 가질 것이다.
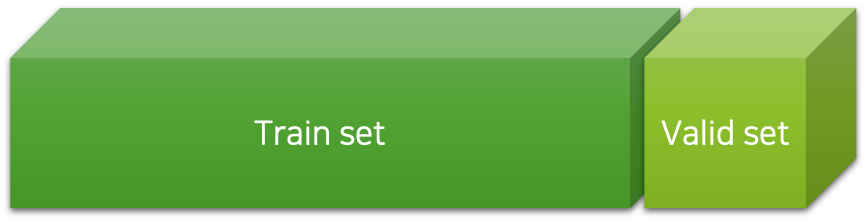
이를 위해서 우리는 학습 데이터를 일부 임의로 나누어 검증 데이터셋을 구성하고
이것을 학습하는 도중에 주기적으로 모델에 넣어 손실 값을 구함으로써,
오버피팅 여부를 확인할 수 있다.
보통 매 에포크마다 이 작업을 수행하며, 이 과정을 검증과정이라 부른다.
또한, 검증 과정에서 얻은 검즘 데이터셋에 대한 손실 값을 검증 손실값이라고 부른다.
여기서 중요한 점은 검증 데이터셋을 통해서는 최적화(학습)를 진행하지 않으며,
데이터셋을 랜덤하게 나누는 과정에서 편향이 있어서는 안된다는 것이다.
결국 우리는 일반화 오차를 최소화 하는 것이 최종 목적이므로, 검증 손실 값을 최소화 하는 것이라고 볼 수 있다.
모델은 학습 데이터에 대해서만 학습된 상태이므로,
검증 데이터셋에 대해서 좋은 예측을 수행한다면 일반화가 잘 되었다고 판단할 수 있다.
또는 만약 학습 오차는 낮지만 검증 오차가 높다면, 일반화가 잘 되고 있지 않다고 판단할 수 있을 것이다.
정리하면 우리는 이와 같이 학습 데이터를 통째로 학습시키는 것이 아닌,
일부를 떼어내어 검증 데이터로 활용함으로써,
모델의 일반화 성능을 측정하고 오버피팅을 피할 수 있다.

전체 학습 과정은 에포크 수 만큼 반복 될 것이고, 이는 위 그림에서 가장 바깥 쪽의 사이클이 의미한다.
또한 한 에포크는 학습 과정과 검증 과정으로 구성되어 있으며,
각각의 학습 과정과 검증 과정은 미니배치로 구성된 여러 이터레이션으로 구성되어 있다.
검증 과정에서는 손실 값을 계산하지만, 역전파 계산과 경사하강법 의 수행이 없는 것에 유의해야 한다.
또한 검증 과정 이후에는
현재 에포크의 검증 손실 값이 기존보다 더 낮아졌는지 확인을 통해, 오버피팅 여부를 체크할 수 있다.
다만 주의할 점은, 모델 최적화 과정에서는 손실 값이 들쑥날쑥 할 수 있기 때문에,
한번 검증 손실 값이 낮아지지 못했다고 오버피팅이라고 볼 수는 없다.
따라서 모든 학습이 종료된 이후에,
최소 검증 손실 값을 기록했던 에포크의 모델 가중치 파라미터를 복원하는 과정을 거쳐야 한다.
이 과정을 거치면 우리는 일반화 오차가 가장 낮은 모델을 선택할 수 있고, 오버피팅을 피할 수 있습니다.
코드구현
아래는 학습 과정 및 검증 과정은 코드로 구현한 것이다.
앞선 코드와 달리 데이터를 분류해야 한다.
이때 학습, 검증, 테스트 데이터 비율은 6:2:2로 설정!
#Train/Valid/Test 분류
#6:2:2로 분류할 예정
ratios=[.6 , .2, .2]
train_cnt=int(data.size(0)*ratios[0])
valid_cnt=int(data.size(0)*ratios[1])
test_cnt=int(data.size(0)*ratios[2])
#랜덤 샘플링으로 데이터 분류
indices=torch.randperm(data.size(0))
x = torch.index_select(x, index=indices, dim=0)
y = torch.index_select(y, index=indices, dim=0)
#split train. valid and test with each count
x =list(x.split(cnt,dim=0))
y =y.split(cnt, dim=0)
데이터를 분류한 다음에는 스케일링을 해줘야 한다.
이때 주의할 점은 정규화 과정은 훈련 데이터에 대해서만 해야한다!
# 스케일링
scaler=StandardScaler()
#훈련데이터에 대해서만 fit을 해야함 scaler=StandardScaler()
scaler.fit(x[0].numpy())
x[0]=torch.from_numpy(scaler.transform(x[0].numpy())).float()
x[1]=torch.from_numpy(scaler.transform(x[1].numpy())).float()
x[2]=torch.from_numpy(scaler.transform(x[2].numpy())).float()
그런 다음 심층신경망을 구현하고 옵티마이저는 Adam으로 설정한다.
# 학습코드 구현
#심층신경망 구현
model=nn.Sequential(nn.Linear(x[0].size(-1),6),nn.LeakyReLU(),
nn.Linear(6,5),nn.LeakyReLU(),
nn.Linear(5,4),nn.LeakyReLU(),
nn.Linear(4,3),nn.LeakyReLU(),
nn.Linear(3,y[0].size(-1)))
optimizer=optim.Adam(model.parameters()
아래는 본격적으로 학습 및 검증 과정을 코드로 구현한 전체 코드이다.
n_epoch=4000
batch_size=256
print_interval=100
#우리가 원하는 모델 == 가장 낮은 검증 손실 값을 갖는 모델
from copy import deepcopy
lowest_loss=np.inf #최저 검증 손실을 추적하기 위한 변수
best_model=None # 최저 검증 손실을 뱉어낸 모델을 저장하기 위한 변수
early_stop=100 #조기종료
lowest_epoch=np.inf #최저 검증 손실 값을 뱉어낸 에포크를 저장하기 위한 변수
train_history, valid_history=[], []
for i in range(n_epoch):
indices=torch.randperm(x[0].size(0)) #인덱스를 섞어줌
x_=torch.index_select(x[0], dim=0, index=indices) #섞어진 인덱스 순으로 재배열
y_=torch.index_select(y[0], dim=0, index=indices)
x_=x_.split(batch_size, dim=0) #미니배치 생성(예를 들어 1000개에 대해서 batch size를 100개로 split하면 10개의 미니 배치가 생성)
y_=y_.split(batch_size, dim=0)
train_loss,valid_loss=0,0
y_hat=[]
#Train Data에 대한 작업 수행 : 가중치 파라미터를 업데이트
for x_i, y_i in zip(x_,y_):
y_hat_i=model(x_i)
loss=F.mse_loss(y_hat_i,y_i)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss+=float(loss) #하나의 epoch에서 나오는 모든 iteration의 loss를 더함
train_loss=train_loss/len(x_) #그리고 평균을 냄 -> 1epoch당 loss
#검증 데이터셋을 활용하여 검증 작업 수행
with torch.no_grad():#그래디언트 계산할 필요없음 : 그저 위에서 뱉어낸 가중치 파라미터를 통해 손실값만 계산해서 최저 손실값을 뱉어낸 모델을 찾으면 된다.
#섞을 필요 x
x_=x[1].split(batch_size,dim=0)
y_=y[1].split(batch_size,dim=0)
valid_loss=0
for x_i, y_i in zip(x_,y_):
y_hat_i=model(x_i)
loss=F.mse_loss(y_hat_i,y_i)
valid_loss+=loss
y_hat += [y_hat_i]
valid_loss=valid_loss/len(x_)
train_history+=[train_loss]
valid_history+=[valid_loss]
if (i+1)% print_interval==0:
print('Epoch %d : train_loss= %.4e valid_loss= %.4e lowest_loss= %.4e' % (i+1, train_loss, valid_loss, lowest_loss))
#학습과 검증이 끝난 후에는 검증 손실 값을 기준으로 모델 저장 여부 판단
#lowest_loss와 현재 검증 손실 값인 valid_loss를 비교하여 갱신될 경우 현재 에포크의 모델을 best_model에 저장
if valid_loss <= lowest_loss:
lowest_loss=valid_loss
lowest_epoch=i
#state_dict(): 현재 모델에 저장되어 있던 key_value들을 반환
best_model=deepcopy(model.state_dict())
else:
if early_stop > 0 and lowest_epoch + early_stop < i+1:
print('There is no improvement during last %d epochs' % (early_stop))
break
print('The best validation loss from epoch %d : %.4e' %(lowest_epoch+1, lowest_loss))
#Load best epoch's model.
model.load_state_dict(best_model)
학습 과정, 검증 과정을 따로 따로 살펴보자!
우선 학습 과정부터 살펴보고자 한다.
< 준비 과정 >
최저 검증 손실 값을 저장할 변수 : lowest_loss
최저 검증 손실 값을 뱉어낸 모델을 저장할 변수 : best_model
최저 손실 값을 뱉어낸 에포크를 저장할 변수 : lowest_epoch
매 에포크마다 train_loss와 valid_loss를 저장할 리스트 : train_history, valid_history
적용 데이터가 전체 데이터가 아닌 위에서 분류한 학습데이터를 적용해야 함
> 즉, x에 대해서 적용해야 하는 것이 아니라 x[0] (전체 데이터의 60프로에 해당)에 적용을 해야 함!
n_epoch=4000
batch_size=256
print_interval=100
#우리가 원하는 모델 == 가장 낮은 검증 손실 값을 갖는 모델
from copy import deepcopy
lowest_loss=np.inf #최저 검증 손실을 추적하기 위한 변수
best_model=None # 최저 검증 손실을 뱉어낸 모델을 저장하기 위한 변수
early_stop=100 #조기종료
lowest_epoch=np.inf #최저 검증 손실 값을 뱉어낸 에포크를 저장하기 위한 변수
train_history, valid_history=[], []
for i in range(n_epoch):
indices=torch.randperm(x[0].size(0)) #인덱스를 섞어줌
x_=torch.index_select(x[0], dim=0, index=indices) #섞어진 인덱스 순으로 재배열
y_=torch.index_select(y[0], dim=0, index=indices)
x_=x_.split(batch_size, dim=0) #미니배치 생성(예를 들어 1000개에 대해서 batch size를 100개로 split하면 10개의 미니 배치가 생성)
y_=y_.split(batch_size, dim=0)
train_loss,valid_loss=0,0
y_hat=[]
#Train Data에 대한 작업 수행 : 가중치 파라미터를 업데이트
for x_i, y_i in zip(x_,y_):
y_hat_i=model(x_i)
loss=F.mse_loss(y_hat_i,y_i)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss+=float(loss) #하나의 epoch에서 나오는 모든 iteration의 loss를 더함
train_loss=train_loss/len(x_) #그리고 평균을 냄 -> 1epoch당 loss학습 과정은 앞에서 그동안 보았던 것과 별 다를 것이 없다.
위 코드처럼 학습 데이터셋을 미니배치로 나누어 한바퀴 학습하고 나면,
검증 데이터셋을 활용하여 검증 작업을 수행한다.
학습과 달리 검증 작업은 역전파를 활용하여 학습을 수행하지 않는다.
따라서 그래디언트를 계산할 필요가 없기 때문에,
torch.no_grad 함수를 호출하여 with 내부에서 검증 작업을 진행한다.
그럼 그래디언트를 계산하기위한 배후 작업들이 없어지기 때문에
계산 오버헤드가 줄어들어 속도가 빨라지고 메모리 사용량도 줄어들게 된다.
그럼 with 내부를 살펴보자!
이때 데이터는 검증 데이터, x[1]에 대해서 작업을 수행해야 한다.
split 함수를 써서 미니배치 크기로 나눠주는 것을 볼 수 있다.
앞서 이야기한 것처럼 검증 작업은 메모리 사용량이 적기 때문에,
검증 작업을 위한 미니배치 크기는 학습용보다 더 크게 가져가도 되지만
간편함을 위해서 그냥 기존 학습용 미니배치 크기와 같은 크기를 사용하겠다.
그리고 학습과 달리 셔플링작업이 빠진 것을 볼 수 있다.
또한 for 반복문 내부에서도 손실값 계산하는 코드만 있고, 역전파 관련 코드는 없는 것을 볼 수 있다.
#검증 데이터셋을 활용하여 검증 작업 수행
with torch.no_grad():#그래디언트 계산할 필요없음 : 그저 위에서 뱉어낸 가중치 파라미터를 통해 손실값만 계산해서 최저 손실값을 뱉어낸 모델을 찾으면 된다.
#섞을 필요 x
x_=x[1].split(batch_size,dim=0)
y_=y[1].split(batch_size,dim=0)
valid_loss=0
for x_i, y_i in zip(x_,y_):
y_hat_i=model(x_i)
loss=F.mse_loss(y_hat_i,y_i)
valid_loss+=loss
y_hat += [y_hat_i]
valid_loss=valid_loss/len(x_)
train_history+=[train_loss]
valid_history+=[valid_loss]
if (i+1)% print_interval==0:
print('Epoch %d : train_loss= %.4e valid_loss= %.4e lowest_loss= %.4e' % (i+1, train_loss, valid_loss, lowest_loss))
학습과 검증 작업이 끝나고 나면, 검증 손실 값을 기준으로 모델 저장 여부를 결정해야 한다.
#학습과 검증이 끝난 후에는 검증 손실 값을 기준으로 모델 저장 여부 판단
#lowest_loss와 현재 검증 손실 값인 valid_loss를 비교하여 갱신될 경우 현재 에포크의 모델을 best_model에 저장
if valid_loss <= lowest_loss:
lowest_loss=valid_loss
lowest_epoch=i
#state_dict(): 현재 모델에 저장되어 있던 key_value들을 반환
best_model=deepcopy(model.state_dict())
else:
if early_stop > 0 and lowest_epoch + early_stop < i+1:
print('There is no improvement during last %d epochs' % (early_stop))
break
print('The best validation loss from epoch %d : %.4e' %(lowest_epoch+1, lowest_loss))
#Load best epoch's model.
model.load_state_dict(best_model)우리가 원하는 것은 검증 손실을 낮추는 것이기 때문에,
따라서 기존 최소 손실 값 변수와 현재 검증 손실 값를 비교하여
최소 손실 값이 갱신될 경우, 현재 에포크의 모델을 저장하면 된다.
> best_model=deepcopy(model.state_dict())
( model.state_dict()는 현재 모델에 저장되어 있는 key_value (가령 가중치 파라미터)들을 반환해준다. )
또한 정해진 기간(early_stop 변수)동안 최소 검증 손실 값의 갱신이 없을 경우, 학습을 종료시킨다.
모든 작업이 수행되고 나면, for 반복문을 빠져나와
best_model에 저장되어있던 가중치 파라미터를 모델 가중치 파라미터로 복원한다.
> model.load_state_dict(best_model)
그럼 우리는 최소 검증 손실 값을 얻은 모델으로 되돌릴 수 있게 된다.
아래는 최종 결과인데, epoch가 453번 돌았을 때
최저 검증 손실 값을 뱉어내었음을 확인할 수 있다.

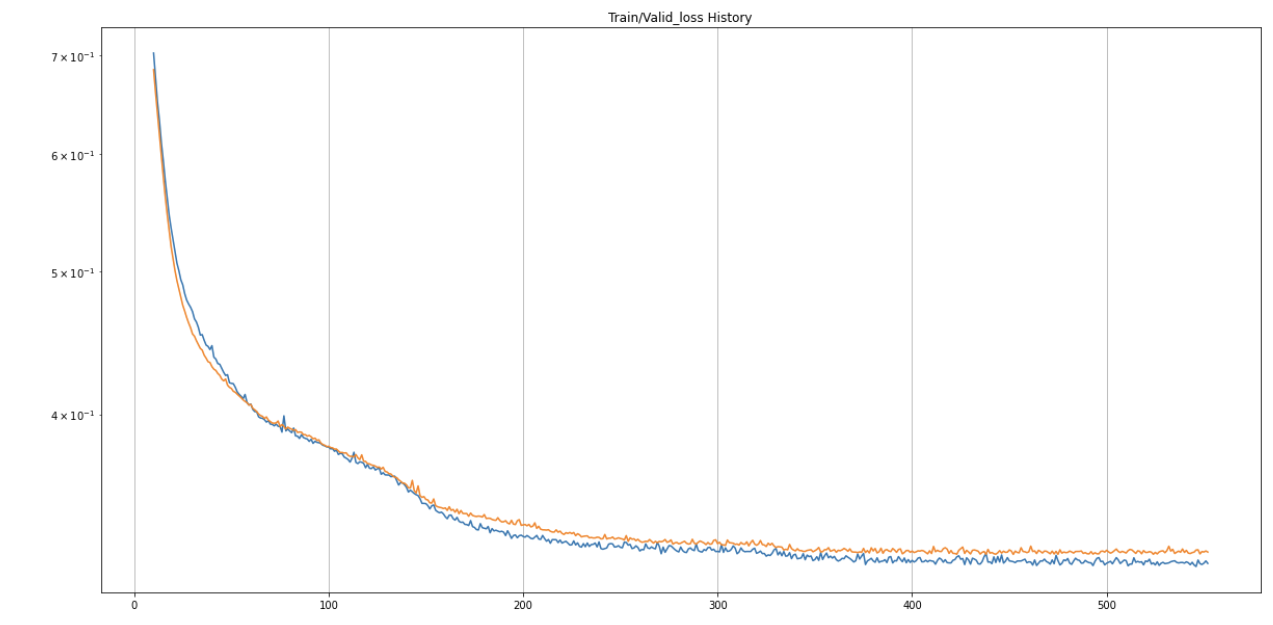
위 과정을 그래프로 나타내면 아래와 같다.
파란색 선이 train_loss이고 주황색 선이 valid_loss이다.
epoch가 진행되면 진행될수록 두개의 값 모두 점점 줄어들고 있음을 확인할 수 있다.
이제 테스트 데이터셋에 대해서도 성능을 확인해보자!
우리의 최종 목표는 테스트 성능이 좋은 모델을 얻는 것이지만,
이 과정에서 학습 데이터셋과 검증 데이터셋만 활용할 수 있었고,
중간 목표는 검증 손실 값을 낮추는 것이었다.
이제 이렇게 얻어진 모델이
테스트 데이터셋에 대해서도 여전히 좋은 성능을 유지하는지 확인해봐야 한다.
#테스트 데이터셋에 대해서도 확인
test_loss=0
y_hat=[]
with torch.no_grad():
x_=x[2].split(batch_size,dim=0)
y_=y[2].split(batch_size,dim=0)
for x_i, y_i in zip(x_,y_):
y_hat_i=model(x_i)
loss=F.mse_loss(y_hat_i,y_i)
test_loss+=loss
y_hat+=[y_hat_i]
test_loss=test_loss/len(x_)
y_hat=torch.cat(y_hat,dim=0)
코드를 보면 검증 작업과 거의 비슷하게 진행되는 것을 볼 수 있다.
이때 데이터는 위에서 분류했던 테스트 데이터에 해당하는 x[2]에 대해서 작업을 수행해야 한다.
검증 과정과 마찬가지로 그래디언트가 필요없기 때문에
torch.no_grad 함수를 활용하여 with 내부에서 작업을 수행해주면 된다.
또한 미니배치 크기로 split하여 for 반복문을 통해서 각 미니배치에 대한 손실값을 계산한다.
마지막으로 sorted 함수를 활용하여
가장 낮은 검증 손실 값과 이에 대응하는 학습 손실 값을 찾아
테스트 손실 값과 함께 출력한다.
#zip(train_history, valid_history)에 대해서 valid_history(즉, x[1]) 을 기준으로 오름차순 정렬
sorted_history=sorted(zip(train_history, valid_history), key=lambda x : x[1])sorted함수는 인수로 데이터와 정렬 기준을 넘겨주면 되는데,
위 코드는 데이터로 train_history와 valid_history의 튜플을 넘겨주고
정렬 기준으로 x[1], valid_history를 기준으로 정렬시켜주는 코드이다.
(디폴트는 오름차순)

'✍️ STUDY > DeepLearning' 카테고리의 다른 글
| [DL] 심층신경망을 활용한 다중분류 (MNIST 실습) (2) | 2023.05.22 |
|---|---|
| [DL] 심층신경망을 활용한 이진분류, 평가지표 (0) | 2023.05.22 |
| [DL] 적응형 학습률, Optimizer (1) | 2023.05.20 |
| [DL] 심층신경망 Basic (0) | 2023.05.19 |
| [DL] 선형회귀, 활성화 함수, 로지스틱 회귀 (0) | 2023.05.19 |
