이번 글에서는
심층신경망을 활용한 분류 문제를 해결하는 방법에 대해서 이야기하고자 한다.
우리는 로지스틱 회귀를 통해 이진 분류문제를 해결하는 것을 배웠다.
마찬가지로 본격적인 분류 문제에 앞서, 특수 케이스인 이진 분류 문제를
심층신경망으로 해결하는 방법에 대해 공부하고자 한다.
로지스틱 회귀
로지스틱 회귀에 대해 간단하게 복습해보자!
로지스틱 회귀는 말만 '회귀'일뿐 사실상 분류 모델이라고 봐도 무방하다.
비선형 함수인 시그모이드를 활성화 함수로 사용하여
최종 출력값이 0~1사이의 값으로 나오게끔 구현되어 있으며
이렇게 나온 결과 값을 임계값을 기준으로 높으면 참, 낮으면 거짓이라고 분류한다.
손실함수로는 선형회귀와 다르게 BCE손실함수를 사용한다는 것을 유의해야 한다.
>그렇다면 심층신경망을 활용하여 이진분류 문제를 어떻게 해결할까?<
매우 간단하다.
심층신경망을 구현하고 마지막에 활성화 함수를 넣어주면 된다.
아래 그림을 보면 더 쉽게 이해할 수 있을 것이다.
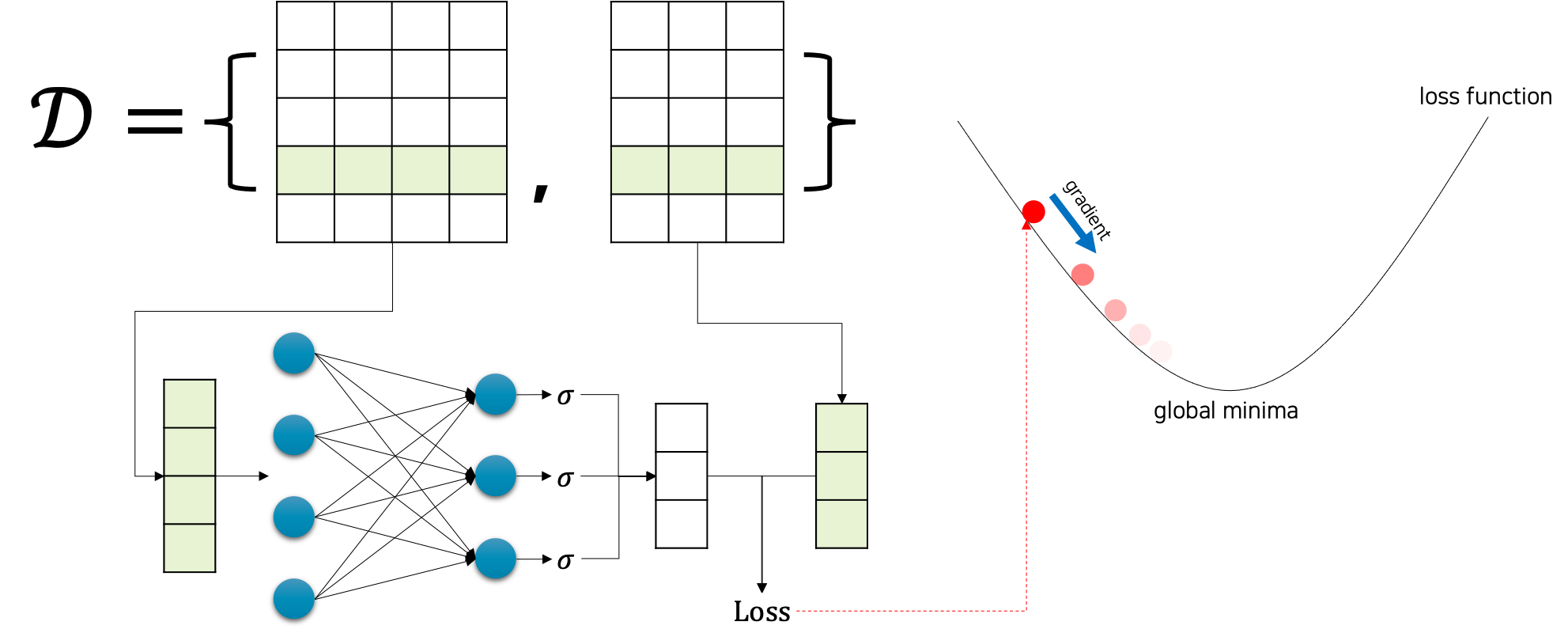
아래 사진과 같이 먼저 심층신경망을 구현한 다음
맨 마지막 계층에 활성화 함수를 넣어주면 끝이다.

평가지표
분류 문제에는 정확도 말고도 다양한 평가지표가 존재한다.
우리는 상황에 맞는 평가지표를 활용할 줄 알아야 한다.
예를 들어 정답 데이터가 한쪽으로 너무 편향된 데이터인 경우에는
평가지표로 정확도를 사용하는 것은 매우 안 좋은 선택이다.
예를 들어 100개의 데이터가 있고 그 중 5개의 데이터만이 오답데이터라고 가정해보자.
이러한 상황 속에서 만약 모든 데이터를 정답 데이터라고 예측했다면
옳게 예측한 레이블은 존재하지 않지만
정확도는 95%로 매우 높은 수치가 나오게 되는 상황이 발생하게 된다.
따라서 우리는 적절한 평가지표를 활용하여 모델의 성능을 판단해야 한다.
평가 지표에 대해 이야기 하기 전에 정답과 예측에 따른 명칭을 먼저 알아야 한다.
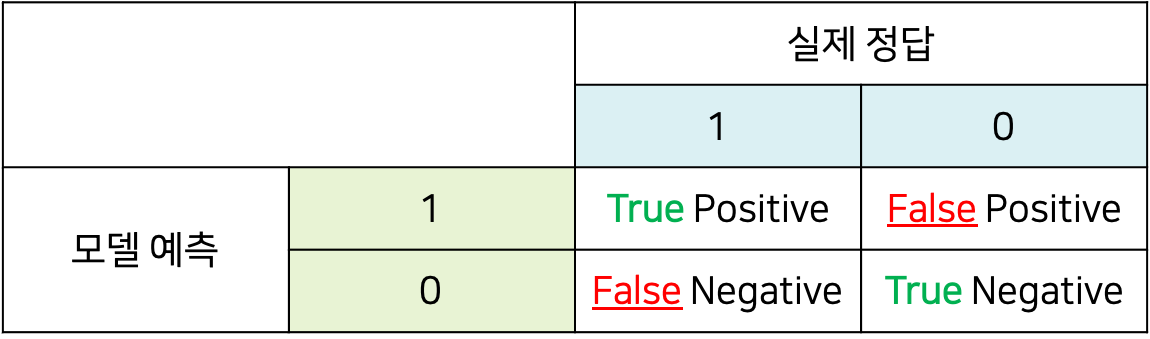
위 사진에서 True Positive는 참인 데이터를 참으로 예측한 데이터를 의미한다.
그리고 False Positive는 잘못된 positive, 즉 거짓인 데이터를 참으로 예측한 데이터들을 의미한다.
False Negative, True Negative도 마찬가지이다.
우리는 4가지를 결과물을 활용하여 다양한 평가지표를 도입할 수 있다.
0. 정확도
‘전체 예측 갯수’와 ‘전체 예측 중에서 실제로 맞춘 참의 갯수’의 비율을 나타낸다.
수식은 아래와 같다.

정밀도 / 재현율
정밀도란 참으로 예측한 데이터 중 실제로 참인 데이터의 비율을 의미하고,
재현율은 실제로 참인 데이터 중 참으로 예측이 된 데이터의 비율을 의미한다.
정밀도와 재현율을 헷갈리지 않게 조심하자!
정밀도와 재현율은 임계값 설정에 따른 상충되던 성능의 명칭이다
임계값을 높게 설정하면 FP의 수치가 높아지기 때문에
저절로 정밀도가 낮아지게 될 것이고,
이는 재현율의 수치를 높이게 한다.
반대로 임계값을 낮게 설정하면 재현율이 낮아지고, 정밀도가 높아지게 된다.

F1 score
정밀도와 재현율처럼 여러개의 점수가 상존한다면 어떤 점수를 기준으로 줄을 세워야 할까?
우리는 결국 1개의 종합 총점을 뽑아내야 한다.
F1 점수도 그런 의미에서
정밀도와 재현율을 기반으로 계산할 수 있는 유용한 지표이다.
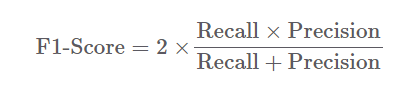
사실 F1의 경우에는 임계값이 고정되어 있을 때, 정밀도와 재현율을 기반으로 계산하게 된다.
따라서 만약 적용되는 임계값이 달라지게 된다면 F1 점수도 바뀌게 되는 상황이 발생한다.
이러한 경우 사용자 입장에서는 F1 점수만으로는 모델의 성능을 파악하기 어려운 상황이 발생하게 된다.
AUROC
앞선 상황에서 필요한 것이 바로 AUROC이다.
AUROC는 변화하는 임계값에 따른 모델의 성능을 나타내며,
모델의 강인함robustness을 알수 있는 척도이기도 한다.

왼쪽 그래프에서 주황색 선의 아래 구간의 넓이를 AUROC라고 한다.
보통 모델이 좋은 성능을 가질수록 주황색 선이 좌상단 꼭지점에 가까이 붙게 되고, 그럴 경우 AUROC의 값은 1이 된다.
반대로 모델이 정답을 그냥 찍는 수준에 가까울 경우, 파란색 점선에 근접하게 되고 AUROC의 값은 0.5가 된다.
코드 구현
코드는 손실함수가 mse가 아닌 BCE로 바뀐 거 빼고는 앞에서 심층신경망을 구현했던 코드와 동일하다.
따라서 테스트 데이터셋에 대한 코드만 설명하겠다.
#테스트 데이터셋에 대해서도 확인
test_loss=0
y_hat=[]
with torch.no_grad():
x_=x[2].split(batch_size,dim=0)
y_=y[2].split(batch_size,dim=0)
for x_i, y_i in zip(x_,y_):
y_hat_i=model(x_i)
loss=F.binary_cross_entropy(y_hat_i,y_i)
test_loss+=loss
y_hat+=[y_hat_i]
test_loss=test_loss/len(x_)
y_hat=torch.cat(y_hat,dim=0)
#zip(train_history, valid_history)에 대해서 valid_history(즉, x[1]) 을 기준으로 오름차순 정렬
sorted_history=sorted(zip(train_history, valid_history), key=lambda x : x[1])위 코드를 보면 손실함수가 이진교차엔트로피, BCE로 바뀐 것을 확인할 수 있다.
이진분류에 대해서 정확도를 한번 구해보자!
로지스틱 회귀는 결과로 확률값을 반환해주기 때문에
이를 이진분류로 적용하기 위해서는
임계값을 기준으로 클래스로 바꿔주는 작업을 거쳐야 한다.
아래 코드를 보면 y_hat에는 확률값이 들어가 있다.
그리고 y에는 0,1 즉 2개의 클래스가 값으로 들어가 있다.
따라서 정확도를 확인하기 위해서
불리언(Boolean) 성질을 이용해야 한다.
#정확도 구하기
correct_cnt=(y[2]==(y_hat>0.5)).sum() # 파이썬에서 1은 True를 의미 -> 따라서 y값이 1이고 y_hat값이 0.5가 넘은 값에 대해서만 sum을 진행
total_cnt=float(y[2].size(0))
print('Test Accuracy : %.4f' % (correct_cnt / total_cnt))
AUROC는 사이킷런에서 제공해주므로 간단하게 구현할 수 있다.
인수로 실제값과 예측값을 넘겨주면 된다.
#AUROC는 사이킷런에서 제공
from sklearn.metrics import roc_auc_score
#인수로 실제값과 예측 값을 넘겨주면 된다
#1에 가까울 수록 좋은 거!
roc_auc_score(df.values[: , 0], df.values[:,1])'✍️ STUDY > DeepLearning' 카테고리의 다른 글
| [DL] 정규화 (Regularization) (0) | 2023.05.23 |
|---|---|
| [DL] 심층신경망을 활용한 다중분류 (MNIST 실습) (2) | 2023.05.22 |
| [DL] 오버피팅(Over Fitting) , 검증(Validation) (1) | 2023.05.20 |
| [DL] 적응형 학습률, Optimizer (1) | 2023.05.20 |
| [DL] 심층신경망 Basic (0) | 2023.05.19 |
