오늘은 차원 축소에 대해 스터디를 한 것을
회고하고자 한다.
차원은 특성(피쳐)의 개수와 연관이 있는데
만약 차원이 너무 커지면 데이터의 크기가 커지게 되고,
이는 데이터 간의 거리가 멀어지게끔 만들어 준다.
데이터의 거리가 멀어지면
거리 기반 알고리즘(예를 들어 knn) 성능이 떨어지게 된다
이처럼 차원이 커지면 전체적으로 알고리즘의 성능이 떨어질 뿐만 아니라
희소행렬이 되어서 정확도가 떨어지게 된다.
그렇다면 우리는 이를 방지하기 위해
차원을 축소해야 한다.
차원축소 방법에는 크게 2가지로 나눌 수 있다.
1. 특성 선택
: 라쏘회귀와 가티 계수(회귀계수)가 0인 피쳐들은
다 제거하거나
또는 우리가 빈도수를 기반으로
너무 적거나 너무 많은 단어들을 제거했던 과정이
특성 선택에 해당
2. 특성 추출
: 새로운 특성을 생성
예를 들어 PCA, LSA와 같은 알고리즘이
특성 추출에 해당
특성 선택은 앞에서 라쏘를 공부하면서 했기 때문에
오늘은 특성 추출에 대해 요약하고자 한다.
PCA를 이용한 차원축소
PCA란?
우리 말로는 “주성분 분석”으로
데이터의 분산을
최대한 많이 반영하는 새로운 축을 찾아
변환함으로써 차원을 축소
차원을 축소할 때 가장 중요한 점이
데이터의 정보량을 최대한 보존해야 한다는 점이다.
통계적으로 봤을 때 데이터의 정보량은
분산을 의미한다.
따라서 차원을 축소할 때
데이터의 분산을 최대한 유지하면서
차원을 축소해야 한다.
#train data & test data 생성
from sklearn.datasets import fetch_20newsgroups
#20개의 토픽 중 선택하고자 하는 토픽을 리스트로 생성
categories = ['alt.atheism', 'talk.religion.misc', 'comp.graphics', 'sci.space']
#학습 데이터셋을 가져옴
newsgroups_train = fetch_20newsgroups(subset='train',
#메일 내용에서 hint가 되는 부분을 삭제 - 순수하게 내용만으로 분류
remove=('headers', 'footers', 'quotes'),
categories=categories)
#검증 데이터셋을 가져옴
newsgroups_test = fetch_20newsgroups(subset='test',
remove=('headers', 'footers', 'quotes'),
categories=categories)
#train set 및 test set에 대해서 독립변수 및 종속변수 분류
X_train = newsgroups_train.data #학습 데이터셋 문서
y_train = newsgroups_train.target #학습 데이터셋 라벨
X_test = newsgroups_test.data #검증 데이터셋 문서
y_test = newsgroups_test.target #검증 데이터셋 라벨
#각 데이터셋에 대해서 카운트벡터 생성
from sklearn.feature_extraction.text import TfidfVectorizer
from nltk.corpus import stopwords
#불용어 생성
cachedStopWords = stopwords.words("english")
from nltk.tokenize import RegexpTokenizer
from nltk.stem.porter import PorterStemmer
RegTok = RegexpTokenizer("[\\w']{3,}") # 정규포현식으로 토크나이저를 정의
english_stops = set(stopwords.words('english')) #영어 불용어를 가져옴
def tokenizer(text):
tokens = RegTok.tokenize(text.lower())
# stopwords 제외 및 단어의 길이가 2인 애들만 가져온다
words = [word for word in tokens if (word not in english_stops) and len(word) > 2]
# porter stemmer 적용
features = (list(map(lambda token: PorterStemmer().stem(token),words)))
return features
tfidf = TfidfVectorizer(tokenizer=tokenizer)
#train_set에 대한 특성 벡터 생성
X_train_tfidf = tfidf.fit_transform(X_train) # train set을 변환
#test_set에 대한 특성 벡터 생성(단 특성 집합의 단어들은 train_set을 기준으로)
X_test_tfidf = tfidf.transform(X_test) # test set을 변환
#LR로 모델 평가
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
LR_clf = LogisticRegression() #분류기 선언
LR_clf.fit(X_train_tfidf, y_train) # train data를 이용하여 분류기를 학습
#예측
LR_preds=LR_clf.predict(X_test_tfidf)
print('#Train set score: {:.3f}'.format(LR_clf.score(X_train_tfidf, y_train)))
print('#Test set score: {:.3f}'.format(accuracy_score(y_test,LR_preds)))
#Train set score: 0.962
#Test set score: 0.761
차원축소를 안 한 데이터를 가지고
Logistic Regression으로 정확도를 평가한 결과
정확도가 0.76정도 나왔음을 확인할 수 있었다.
이번에는 PCA를 통해 차원축소를 해보자.
사이킷런에서 PCA를 제공
축소하고자 하는 차원의 크기를 n_components에 넘겨주면 된다
이때, PCA는 인수로 벡터를 못 받음
따라서 toarray()를 이용하여 카운트벡터를 행렬로 바꾼 다음 인수로 넘겨줘야 한다
그리고 카운트벡터와 마찬가지로
train 에 대해서만 fit_transform()적용해야 하며
test에 대해서는 transform()만 적용해야 한다.
그리고 PCA에서는 explained_variance_ratio_를 제공해주는데
이는 각각의 차원이 원본 데이터 분삭을 얼마만큼 반영하는지 알려준다.
explained_variance_ratio_.sum()을 이용하면
축소된 차원의 원본 데이터 분산에 대한 총 반영 비율을
알려준다.
차원을 2000개로 제한해보자.
:n_components에 2000을 넘겨주면 된다.
from sklearn.decomposition import PCA
#n_components는 축소하고자 하는 차원의 크기를 넘겨주면 된다
pca = PCA(n_components=2000, random_state=7)
#PCA는 벡터를 인수로 받을 수 없음 -> 따라서 카운트벡터나 TF-idf로 반환된 벡터를 toarray()로 행렬로 바꾼 후 인수로 넘겨줘야 한다
X_train_pca = pca.fit_transform(X_train_tfidf.toarray())
X_test_pca = pca.transform(X_test_tfidf.toarray())
print('Original tfidf matrix shape:', X_train_tfidf.shape)
print('PCA Converted matrix shape:', X_train_pca.shape)
print('Sum of explained variance ratio: {:.3f}'.format(pca.explained_variance_ratio_.sum()))
Original tfidf matrix shape: (2034, 20085)
PCA Converted matrix shape: (2034, 2000)
Sum of explained variance ratio: 1.000
PCA를 진행하니까 크기가 (2034,20085)에서 (2034,2000)으로 줄어듬
즉 차원이 축소가 되었다.
explained_variance_ratio_ 분산의 비율을 살펴 본 결과
결과값이 1로 차원축소하기 전
데이터의 정보를 100프로 반영한다는 것을 알게됨
이 말은 즉 정보 손실량이 거의 없다는 뜻이다.
#차원축소 후 정확도 측정
#차원축소 후 정확도 측정
LR_clf.fit(X_train_pca, y_train)
#예측
LR_preds_pca=LR_clf.predict(X_test_pca)
print('#Train set score: {:.3f}'.format(LR_clf.score(X_train_pca, y_train)))
print('#Test set score: {:.3f}'.format(accuracy_score(y_test,LR_preds_pca)))
#Train set score: 0.962
#Test set score: 0.761정확도는 차원축소하기 전과 동일
하지만 앞에서 라쏘 모델을 통해 특성의 수를 2000개로 제한했을 때 (특성 선택)
정확도는 0.734였던 것을 생각해보면
특성 추출(PCA)이 더 좋은 성능을 보인다는 것을 확인
특성 선택 vs 특성 추출
특성 선택과 특성 추출 중 어떤 것이 더 성능이 좋을까?
비교하기 위해
특성 선택으로는 라쏘회귀모델을
특성 추출로는 PCA를 이용하여 비교하고자 한다.
<특성 선택 - 라쏘 회귀>
#라쏘회귀 -> 특성 선택
lasso_clf = LogisticRegression(penalty='l1', solver='liblinear', C=1)
#모델 훈련
lasso_clf.fit(X_train_tfidf, y_train)
#예측
lasso_preds=lasso_clf.predict(X_test_tfidf)
print('#Train set score: {:.3f}'.format(lasso_clf.score(X_train_tfidf, y_train)))
print('#Test set score: {:.3f}'.format(accuracy_score(y_test,lasso_preds)))
import numpy as np
# 계수(coefficient) 중에서 0이 아닌 것들의 개수를 출력
print('#Used features count: {}'.format(np.sum(lasso_clf.coef_ != 0)), 'out of', X_train_tfidf.shape[1])
#Train set score: 0.790
#Test set score: 0.718
#Used features count: 321 out of 20085
정확도를 보면 약 0.72가 나왔음을 알 수 있다.
그리고 회귀계수가 0이 아닌 피쳐들은(최종적으로 사용된 특성의 개수)
총 20085개 중 321개밖에 없다는 것을 확인할 수 있었다.
정확한 비교를 위해 PCA를 통해 차원을 321개로 축소해보자.
<특성 추출 - PCA>
라쏘회귀와 차원의 크기는 동일하지만 성능이 훨씬 더 좋음
⇒ 특성 선택보다는 특성추출이 전반적으로 성능이 더 좋음
#위에서 계수가 0인 아닌 애들이 321개 -> 차원을 321개로 축소하고자 함(PCA이용)
pca = PCA(n_components=321, random_state=7)
#pca : array를 인수로 받음
X_train_pca = pca.fit_transform(X_train_tfidf.toarray())
X_test_pca = pca.transform(X_test_tfidf.toarray())
print('PCA Converted X shape:', X_train_pca.shape)
#explained_variance_ratio_ : 차원축소한 애들이 원본 데이터에 대해서 얼마만큼의 분산을 유지했는가를 비율로 나타내줌
#1이면 100프로 보존했다는 뜻
print('Sum of explained variance ratio: {:.3f}'.format(pca.explained_variance_ratio_.sum()))
LR_clf.fit(X_train_pca, y_train)
LR_preds_pca=LR_clf.predict(X_test_pca)
print('#Train set score: {:.3f}'.format(LR_clf.score(X_train_pca, y_train)))
print('#Test set score: {:.3f}'.format(accuracy_score(y_test,LR_preds_pca)))
PCA Converted X shape: (2034, 321)
Sum of explained variance ratio: 0.437
#Train set score: 0.875
#Test set score: 0.751
위에서 차원축소를 2000으로 설정했을 때보다
분산의 비율은 1에서 약0.4로 많이 떨어졌지만
성능은 0.76에서 0.75로 약 1프로 밖에 안 떨어졌다.
✔️ n_components를 100으로 설정
→ n_components를 321으로 설정한 것보다는 아니지만 여전히 라쏘보다는 성능이 더 좋게 나옴
#차원의 크기를 100으로 줄여보자
pca = PCA(n_components=100, random_state=7)
#pca는 인수로 벡터를 안 받고 행렬을 받음 -> toarray()를 이용
X_train_pca = pca.fit_transform(X_train_tfidf.toarray())
X_test_pca = pca.transform(X_test_tfidf.toarray())
print('PCA Converted X shape:', X_train_pca.shape)
print('Sum of explained variance ratio: {:.3f}'.format(pca.explained_variance_ratio_.sum()))
LR_clf.fit(X_train_pca, y_train)
LR_pca_preds=LR_clf.predict(X_test_pca)
print('#Train set score: {:.3f}'.format(LR_clf.score(X_train_pca, y_train)))
print('#Test set score: {:.3f}'.format(accuracy_score(y_test,LR_pca_preds)))
PCA Converted X shape: (2034, 100)
Sum of explained variance ratio: 0.211
#Train set score: 0.807
#Test set score: 0.738
LSA를 이용한 차원 축소와 의미 파악
LSA: 잠재 의미 분석
문서에 잠재된 의미를 분석하고 동시에 단어에 잠재된 의미 또한 분석
LSA는 SVD(특잇값 분해)를 통해 구현이 된다
더 자세히 말하자면 truncated svd(절단된 특잇값 분해)을 통해 구현이 된다.
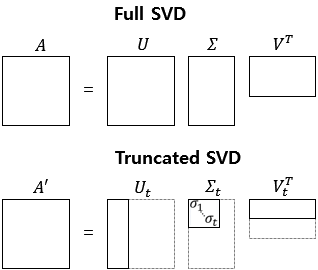
특잇값 분해
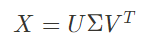
세개의 행렬의 곱으로 이루어짐
:: U(mxm)와V^T(nxn)는 직교행렬, Σ(mxn)는 대각 행렬
⇒ 이때 중간에 있는 Σ가 차원을 축소해주는 key행렬이다
⇒ 즉, LSA를 통해 우리가 원하는 것은 이것을 k개의 차원으로 축소하는 것
⇒ 절단된 특잇값 분해(상위k개만)
위 식에서 X(mxn)는 tfidf벡터로 이루어진 행렬 또는 문서의 카운트 벡터라고할 때,
각 문서(m개)는 n개의 단어 빈도를 통해 표현(mxn)
(U는 문서 원본에 대한 벡터
V^T는 축소되기 전 특성 단어에 대한 벡터)
key 행렬 : Σ
⇒ Σ 에 있는 대각 원소들을 특잇값이라고 부름
⇒ PCA의 결과와 동일한 정보가 들어감.
즉 데이터의 정보량을 가장 잘 보존한 축이 위에 있고,
아래로 점차 줄어드는 형태로 새로운 축에 대한 정보가 들어간다.
절단된 특잇갑 분해
Σ의 대각 원소인 특잇값에서 상위 k개만 골라냄
U에서는 k개의 열만, V^T에서는 k개의 행만 남게 된다
Full SVD일 경우에는 데이터 복원이 가능하지만
절단된 특잇값 분해일 경우 완전한 복원은 불가능하지만 최대한 복원을 하고자 함
⇒ 정보 손실이 어쩔 수 없이 발생
LSA에서 축소된 차원은 잠재된 의미를 나타냄
→ 즉 문서 벡터가 m개의 차원일 때에는(축소되기 전) 사용된 단어의 빈도에 기반해 문서를 표현하지만(mxn),
k개의 차원으로 축소한 후에는 k개의 잠재된 의미의 비중으로 각 문서를 표현
(축소된 차원 k개가 각 문서를 표현해야 함)
⇒ 다시 말해서 k 개의 축소된 차원은 각각 잠재된 의미를 표현하고 있으며,
이를 단어에 대해서 적용하면
각 단어도 k개의 잠재된 의미의 비중으로 표현돼 있다고 해석할 수 있음
LSA를 통한 차원 축소와 성능
PCA와 달리 벡터에 대해서 바로 연산 가능 -> 인수로 카운트 벡터를 주면 된다
⇒ PCA에서는 toarray()를 이용하여 행렬 형태로 바꿨는데 여기서는 그럴 필요없다!
TruncatedSVD를 통해 구현
:객체를 생성할 때
n_components인수에 축소할 차원의 개수를 넘겨주면 된다.
#LSA
from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=2000, random_state=7) #압축할 component의 수 지정
#toarray()이용 안 하고 바로 벡터를 넘겨줌
X_train_lsa = svd.fit_transform(X_train_tfidf)
X_test_lsa = svd.transform(X_test_tfidf)
print('LSA Converted X shape:', X_train_lsa.shape)
print('Sum of explained variance ratio: {:.3f}'.format(svd.explained_variance_ratio_.sum()))
LR_clf.fit(X_train_lsa, y_train)
LR_preds_lsa=LR_clf.predict(X_test_lsa)
print('#Train set score: {:.3f}'.format(LR_clf.score(X_train_lsa, y_train)))
print('#Test set score: {:.3f}'.format(accuracy_score(y_test, LR_preds_lsa)))
LSA Converted X shape: (2034, 2000)
Sum of explained variance ratio: 1.000
#Train set score: 0.962
#Test set score: 0.761
PCA결과와 비교해보면
정확도도 0.761로 동일하고,
축소된 차원의 원본 데이터 분산 반영 비율도 1로 동일
사이킷런에서 자연어처리를 할 때
PCA보다 Truncated SVD를 사용하는 것이 일반적
✔️ 100개 차원으로 축소
svd = TruncatedSVD(n_components=100, random_state=1) #압축할 component의 수 지정
X_train_lsa = svd.fit_transform(X_train_tfidf)
X_test_lsa = svd.transform(X_test_tfidf)
print('LSA Converted X shape:', X_train_lsa.shape)
print('Sum of explained variance ratio: {:.3f}'.format(svd.explained_variance_ratio_.sum()))
LR_clf.fit(X_train_lsa, y_train)
LR_preds_lsa=LR_clf.predict(X_test_lsa)
print('#Train set score: {:.3f}'.format(LR_clf.score(X_train_lsa, y_train)))
print('#Test set score: {:.3f}'.format(accuracy_score(y_test,LR_preds_lsa)))
LSA Converted X shape: (2034, 100)
Sum of explained variance ratio: 0.209
#Train set score: 0.810
#Test set score: 0.745
LSA를 이용한 의미 기반의 문서 간 유사도 계산
단어의 빈도수가 아니라 잠재된 의미의 비중을 이용하여 유사도 계산
→ LSA로 축소된 문서의 벡터는 단어의 빈도수가 아니라
잠재된 의미의 비중으로 표현되어 있기 때문에
이를 이용하여 유사도를 계산
#첫번째 문서와 전체 문서에 대한 유사도 계산
→ 만약 유사도가 잘 나온다면
첫번째 문서와 카테고리가 동일한 문서들이 유사도가 높게 나올 것이다.
from sklearn.metrics.pairwise import cosine_similarity
print('#사용된 전체 카테고리:', newsgroups_train.target_names)
print('#첫 문서의 카테고리:', y_train[0])
#첫번째 문서와 전체 문서에 대한 유사도 비교 -> 이때 cosine similarity는 인수로 벡터를 받음
#변환된 count vector와 기존 값들과의 similarity 계산
sim_result = cosine_similarity([X_train_lsa[0]], X_train_lsa)
#사용된 전체 카테고리: ['alt.atheism', 'comp.graphics', 'sci.space', 'talk.religion.misc']
#첫 문서의 카테고리: 1
sim_result # 첫번째 문서와 전체 문서에 대한 유사도 결과가 반환이 된다.
array([[1. , 0.03997949, 0.0188936 , ..., 0.18398695, 0.01109302,
0. ]])sim_result에는
target문서와 전체 문서간의 유사도 비율이 들어가 있다.
지금부터 sorted를 통해 유사도 결과를 정렬하고,
argsort를 통해 유사도가 높은 문서들의 인덱스를 얻을 것이다.
그 후 위에서 얻은 인덱스를 이용하여 해당 문서의 카테고리를 확인할 예정이다.
#sorted를 통해 정렬(reverse=True로 설정해서 내림차순으로 정렬)
print("#Top 20 유사도(lsa):\\n", sorted(sim_result[0].round(2), reverse=True)[:20])
print('\\n')
#argsort는 오름차순정렬하고 인덱스를 반환
#우리는 내림차순으로 정렬하고 싶기때문에 -를 붙임
sim_index = (-sim_result[0]).argsort()[:20]
print('#Top 20 유사 뉴스의 인덱스(lsa):\\n', sim_index)
print('\\n')
sim_labels = [y_train[i] for i in sim_index]
print('#Top 20 유사 뉴스의 카테고리(lsa):\\n', sim_labels)
#Top 20 유사도(lsa):
[1.0, 0.74, 0.74, 0.72, 0.7, 0.7, 0.69, 0.67, 0.66, 0.65, 0.65, 0.65, 0.63, 0.62, 0.62, 0.62, 0.57, 0.57, 0.55, 0.54]
#Top 20 유사 뉴스의 인덱스(lsa):
[ 0 1957 1674 501 1995 1490 790 1902 1575 1209 1728 892 1892 998
1038 1826 1290 1089 867 151]
#Top 20 유사 뉴스의 카테고리(lsa):
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
첫번째 문서 카테고리 라벨이 1이었는데, 유사도 분석한 결과 유사도가 높은 문서의 카테고리도 1임
#차원축소 안 하고 유사도 계산
→ 빈도수 기반
lsa로 차원축소한 뒤 코사인 유사도 계산한 것과 마찬가지로
첫번째 문서와 유사도가 가장 높은 문서들의 카테고리가 1임
하지만, 유사 문서의 인덱스의 순서들이 다르다는 점!
또한 lsa에서는 자기 자신을 제외하고 가장 높은 유사도가 0.7정도였고
가장 낮은 유사도가 0.5정도였는데,
차원축소를 안 하고 유사도 계산 결과를 보면 가장 높은 유사도 수치가 0.3밖에 안된다
⇒ 특성이 너무 많아서 차원의 저주때문에!!
#차원축소 안 하고 코사인 유사도 계산
sim_result = cosine_similarity(X_train_tfidf[0], X_train_tfidf)
print("#Top 20 유사도(tfidf):\\n", sorted(sim_result[0].round(2), reverse=True)[:20])
sim_index = (-sim_result[0]).argsort()[:20]
print('\\n')
print('#Top 20 유사 뉴스의 인덱스(tfidf):\\n', sim_index)
print('\\n')
sim_labels = [y_train[i] for i in sim_index]
print('#Top 20 유사 뉴스의 카테고리(tfidf):\\n', sim_labels)
#Top 20 유사도(tfidf):
[1.0, 0.3, 0.22, 0.21, 0.19, 0.19, 0.19, 0.17, 0.16, 0.16, 0.16, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.14]
#Top 20 유사 뉴스의 인덱스(tfidf):
[ 0 1575 1892 1490 501 1290 1013 998 1636 1705 1995 1957 1664 651
1038 429 1089 1209 1728 1803]
#Top 20 유사 뉴스의 카테고리(tfidf):
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
LSA 를 통한 단어간 유사도 파악
LSA에서는 문서 간의 유사도뿐만 아니라
단어간의 유사도 또한 파악할 수 있다.
카운트 벡터 행렬을 단어의 관점에서 보면
하나의 단어는 모든 문선에 나타난 빈도로 표현되고 있음
따라서 문서에 나타나는 빈도 분포에 따라 단어 간의 유사도를 구할 수 있음
LSA에서는 문서가 축소된 의미의 비중으로 표현되므로
이를 이용하여 단어 간의 의미적인 유사도를 구할 수 있다.
※ svd.components_
각 차원에 대한 단어들의 비중을 의미 :: V(k)^T
※ svd.singular_values
Σ(k)의 대각 원소들을 반환
※ np.diag(svd.singularvalues).dot(svd.components_)
각 차원에 대한 단어들의 "잠재된 의미의" 비중 :: Σ(k) * V(k)^T
np.diag(array)
→ array가 (n,1)형태 : array를 대각행렬로 만들어줌
→ array가 (mxn)일 때 : 대각 원소만 뽑아서 반환
tfidf = TfidfVectorizer(max_features=1000, min_df=5, max_df=0.5)
X_train_tfidf = tfidf.fit_transform(X_train) # train set을 변환
svd = TruncatedSVD(n_components=100, random_state=1) #압축할 component의 수 지정
X_train_lsa = svd.fit_transform(X_train_tfidf)
print('#components_의 shape:', svd.components_.shape) # (100,1000)
print('#singular_values_의 shape:', svd.singular_values_.shape)
t_words = np.diag(svd.singular_values_).dot(svd.components_).T #단어들의 잠재된 의미의 비중
print('#변환된 단어-잠재의미 행렬의 shape:', t_words.shape) #1000개의 단어에 대해 100개의 내재된 의미
#components_의 shape: (100, 1000)
#singular_values_의 shape: (100,)
#변환된 단어-잠재의미 행렬의 shape: (1000, 100)
원본 데이터 크기 (20085,1000)
100개의 차원으로 축소 > (20085,100)
np.where( ) : 조건을 만족하는 인덱스를 가져옴
np.where(tfidf.get_feature_names_out()=='space') #조건에 만족하는 인덱스 반환
(array([812], dtype=int64),)
np.where(tfidf.get_feature_names_out()=='space')[0][0]
812
특성으로 사용된 단어 space와
비슷한 특성 단어를 유사도 계산을 통해 파악
( 이때 cosine similarity의 인수로
축소된 차원에 대한 단어들의 잠재된 의미의 비중을 인수로 넘겨줌
> 크기 (특성 단어의 개수, 축소된 차원의 개수) )
=>그러니까 각 행이 특정 단어에 대한 축소된 차원의 잠재된 의미의 비중을 의미) )
# space에 해당하는 벡터를 가져옴
#np.where : 조건에 만족하는 인덱스 반환
source = t_words[np.where(tfidf.get_feature_names_out() == 'space')[0][0]]
sim_result = cosine_similarity([source], t_words) #변환된 count vector와 기존 값들과의 similarity 계산
print("#Top 20 유사도(tfidf):", sorted(sim_result[0].round(2), reverse=True)[:20])
sim_index = (-sim_result[0]).argsort()[:20]
print('#Top 20 유사 뉴스의 인덱스(tfidf):', sim_index)
sim_labels = [tfidf.get_feature_names_out()[i] for i in sim_index]
print('#Top 20 유사 뉴스의 카테고리(tfidf):', sim_labels)
#Top 20 유사도(tfidf): [1.0, 0.73, 0.72, 0.69, 0.66, 0.58, 0.56, 0.56, 0.54, 0.54, 0.52, 0.52, 0.52, 0.51, 0.51, 0.5, 0.5, 0.49, 0.48, 0.47]
#Top 20 유사 뉴스의 인덱스(tfidf): [812 314 754 829 594 679 720 650 785 565 101 435 606 545 854 746 669 856
611 564]
#Top 20 유사 뉴스의 카테고리(tfidf): ['space', 'exploration', 'sci', 'station', 'office', 'propulsion', 'reports', 'planetary', 'shuttle', 'national', 'astro', 'international', 'operations', 'missions', 'technical', 'satellites', 'probes', 'telescope', 'orbiter', 'nasa']
TSNE를 이용한 시각화
tSNE는 시각화를 위해 사용되는 알고리즘이다.
(from sklearn.manifold import TSNE)
2차원으로 표현하는 것이 일반적이며
객체를 생성할 때 n_components=2 를 넘겨주면 된다.
사용법은 TruncatedSVD와 유사함
#차원축소 x
plt.text(x,y,label,color) : 좌표(x,y)에 색깔은 color으로 label을 찍어라!
from sklearn.manifold import TSNE
tfidf = TfidfVectorizer(tokenizer=tokenizer)
X_train_tfidf = tfidf.fit_transform(X_train) # train set을 변환
X_test_tfidf = tfidf.transform(X_test) # test set을 변환
tsne = TSNE(n_components=2, random_state=7)
tsne_tfidf = tsne.fit_transform(X_train_tfidf)
print('TSNE dimension:', tsne_tfidf.shape)
def tsne_graph(tsne_2, label, lim=None):
colors = {0:'blue', 1:'red', 2:'green', 3:'purple'}
x = tsne_2[:,0] #압축된 첫 차원을 x좌표로 이용
y = tsne_2[:,1] #압축된 둘째 차원은 y좌표로 이용
plt.figure(figsize=(15,10)) #그래프 크기지정
if lim == None: #축의 범위를 지정 안 해줬으면 x좌표와 y좌표의 최소,최대값으로 범위를 설정해준다.
lim = [min(x), max(x), min(y), max(y)]
plt.xlim(lim[0], lim[1]) #x축의 범위
plt.ylim(lim[2], lim[3]) #y축의 범위
#for i in range(500):
for i in range(len(x)):
if (lim[0] < x[i] < lim[1]) and (lim[2] < y[i] < lim[3]):
#위치 x[i],y[i]에 색깔은 color[i]로 label[i]를 text로 쓰면서 좌표평면에 찍어라
plt.text(x[i], y[i], label[i], color = colors[label[i]])
plt.show()
tsne_graph(tsne_tfidf, y_train, (-4, 5, -5, 5))TSNE dimension: (2034, 2)
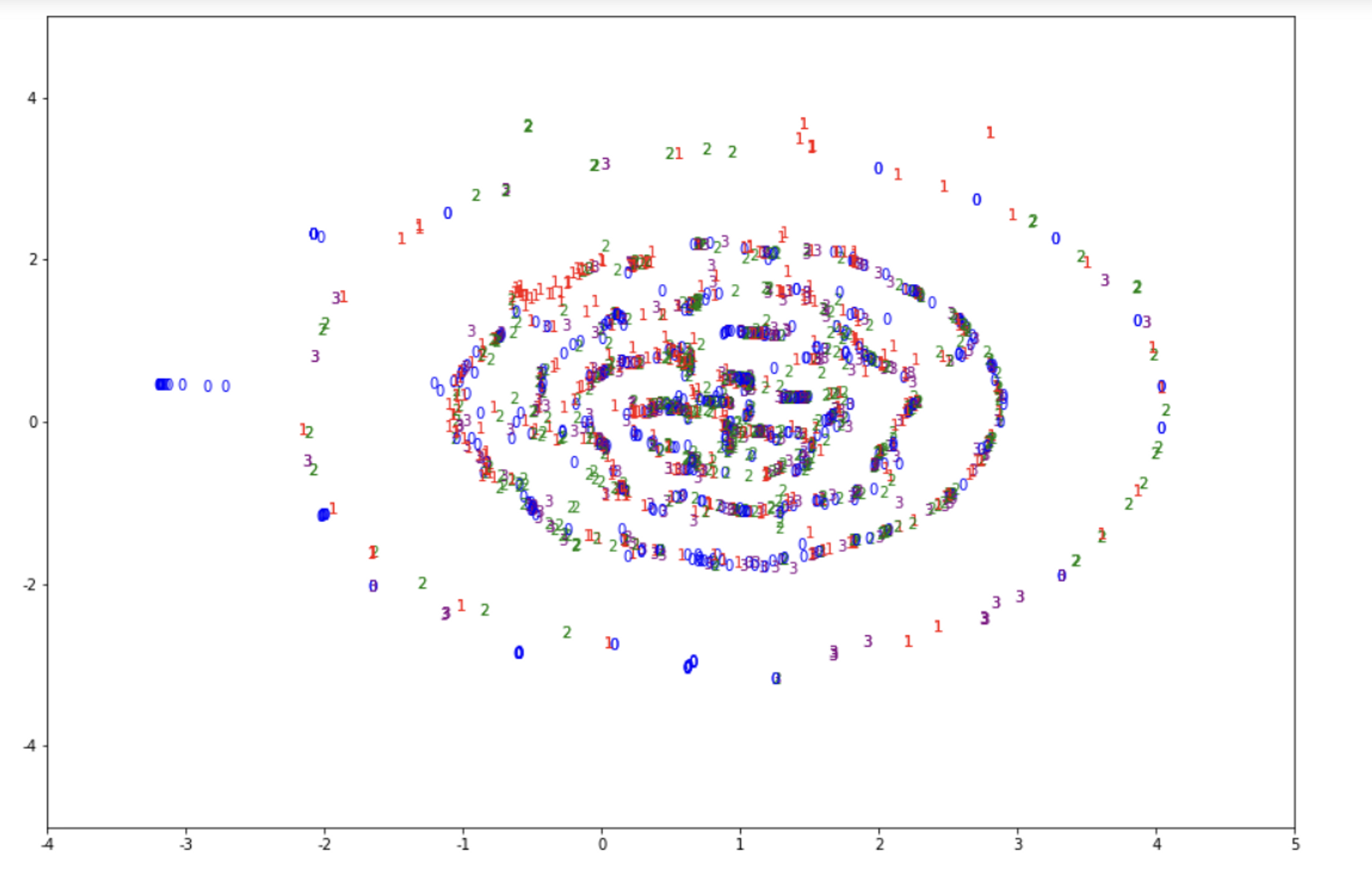
#차원축소 o
LSA로 차원축소 한 것이 더 잘 분류가 되었음 → 위에서 유사도 계산한 결과의 증명
svd = TruncatedSVD(n_components=100, random_state=1) #압축할 component의 수 지정
X_train_lsa = svd.fit_transform(X_train_tfidf)
X_test_lsa = svd.transform(X_test_tfidf)
print('LSA Converted X shape:', X_train_lsa.shape)
print('Sum of explained variance ratio: {:.3f}'.format(svd.explained_variance_ratio_.sum()))
tsne_lsa = tsne.fit_transform(X_train_lsa)
print('TSNE dimension:', tsne_lsa.shape)
print('#Selected categories:', newsgroups_train.target_names)
tsne_graph(tsne_lsa, y_train)
LSA Converted X shape: (2034, 100)
Sum of explained variance ratio: 0.209
TSNE dimension: (2034, 2)
#Selected categories: ['alt.atheism', 'comp.graphics', 'sci.space', 'talk.religion.misc']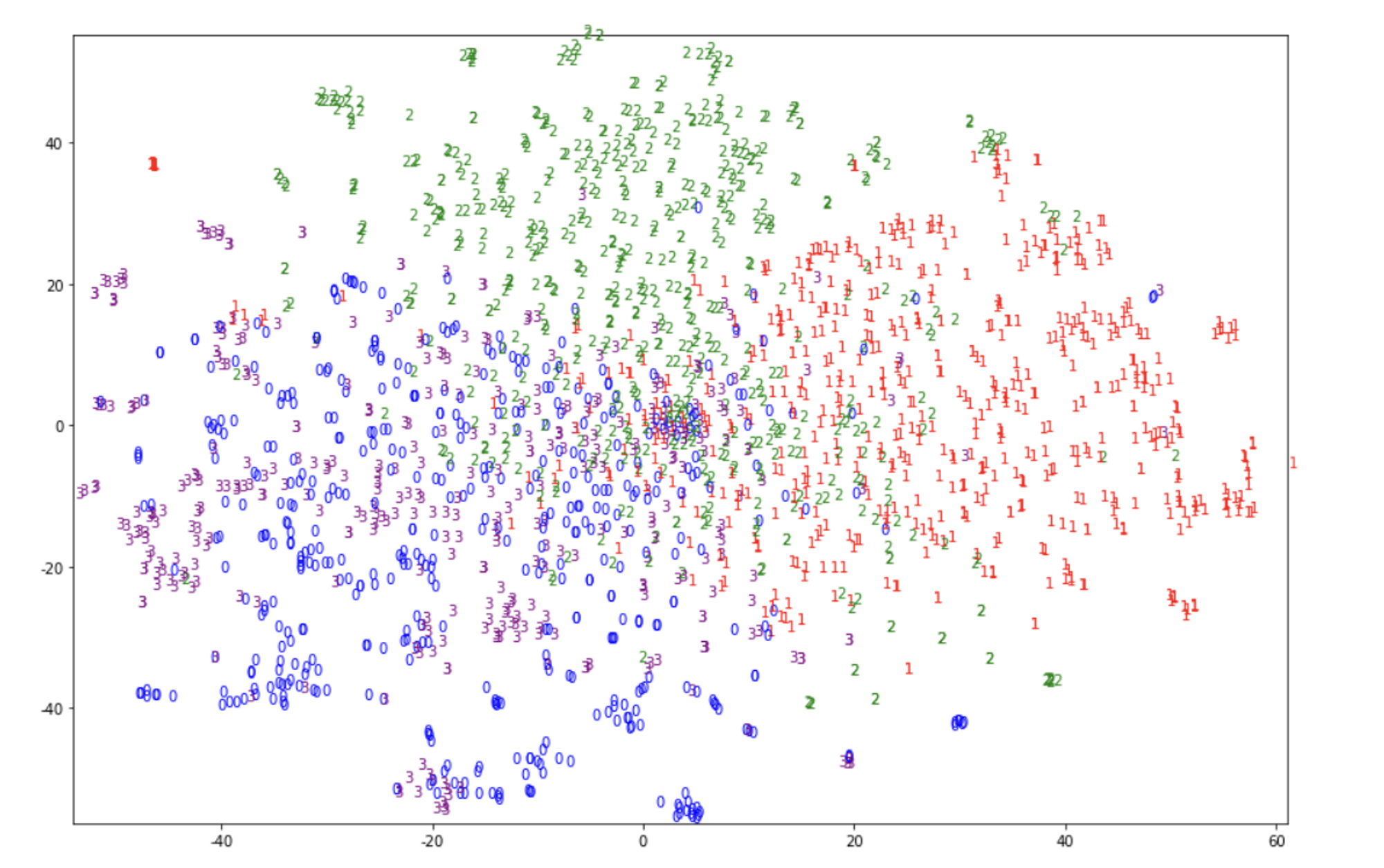
'✍️ STUDY > NLP' 카테고리의 다른 글
| [Text Mining] 감성분석 (1) | 2023.03.22 |
|---|---|
| [Text Mining] 토픽모델링 (0) | 2023.03.08 |
| [Text Mining] BOW 기반의 문서 분류 (0) | 2023.02.21 |
| [Text Mining] CountVectorizer와 TF-IDF (0) | 2023.02.13 |
| [Text Mining] 텍스트 전처리, 자연어 전처리 (0) | 2023.02.06 |
